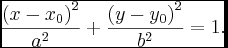Orbits are usually ellipses
The first relevant fact is that most celestial orbits are ellipses.
Well, there are a few objects that enter our solar system, loop around the sun, and then are never heard from again. They may have orbits that are not ellipses (or they may be ellipses with such long periods that astronomers have not detected their location after some historical observation).
Basic Algebra of Ellipses
Algebra teachers in the “olden days” once drew ellipses on the chalk board with a piece of string and something to represent the two foci. This demonstrated the key basic idea about constructing an ellipse.
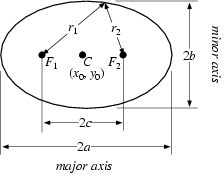
An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r1 and r2 from two fixed points F1 and F2 (the foci) separated by a distance of 2c is a given positive constant 2a. This results in the two-center bipolar coordinate equation
r1 + r2 = 2a
where a is the semi-major axis (i.e., half the major axis) and the origin of the coordinate system is at one of the foci. The corresponding parameter is known as the semi-minor axis.