There are five elements of a Keplerian elliptical orbit.
Two parameters determine the position of the plane of the object’s orbit relative to the plane of the Earth’s orbit. (Remember that the plane of the Earth’s orbit is called the “ecliptic.”) Since the sun is the common focal point of both orbits, the two orbital planes intersect in a line, called the line of nodes. The two parameters describing the object’s plane are:
- i—the angle of inclination (the angle between the planes)
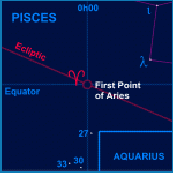
- Θ—the angle made by the line of nodes with some fixed axis in the plane of the Earth’s orbit. The usual point chosen is the First Point of Aries , one of the two points on the celestial sphere where the Ecliptic and the celestial equator cross one another. The First Point of Aries, which is actually in Pisces, defines the zero-point for right ascension. One parameter specifies the angle which the main axis of the object’s orbit within its own orbital plane makes with the line of intersection with the Earth’s orbit:
- phi—for this parameter, we take the angle between the
major axis of the object’s orbit and the line of nodes.