Here we will explain a bit about the coordinate systems that astronomers employ. Then we explore how to best think about the data that we can collect, given the view that we have from Earth into space.

 Celestial Sphere

One of the coordinate systems very relevant to us is the celestial sphere, used by astronomers to describe directions of the stars and other astronomical objects in relation to the Earth.

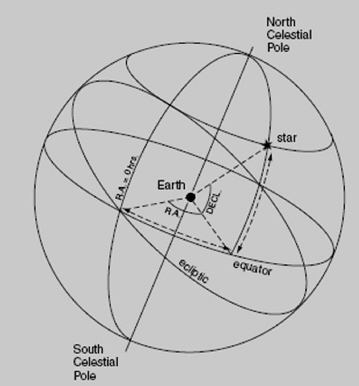
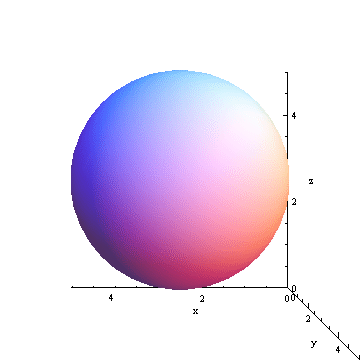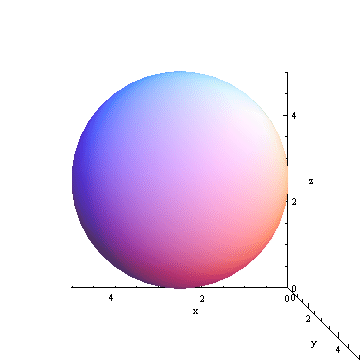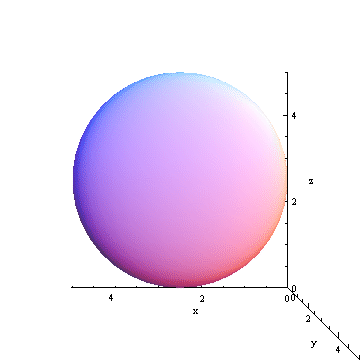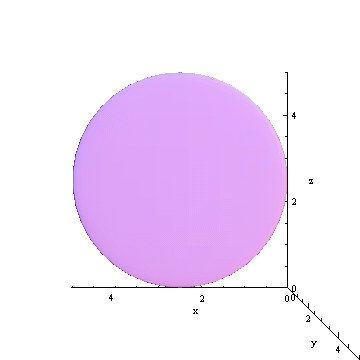This system has been used by astronomers since ancient times. It is an x-y coordinate system, recorded as the intersection of two circles on an imaginary sphere. The observer is at the center (i.e., on Earth looking out).

The circles are lines of longitude and latitude. One set of circles runs perpendicular to the celestial equator, ascending overhead from the observer’s horizon. So for example, for an observer at the Earth’s equator, the lines of “right ascension” (measured in hours, minutes, and seconds) record objects apparently rising in the east. The other set of circles runs parallel to the celestial equator (declination, measured in degrees).

But this is the key point: from our view on Earth, looking out at a spot in space, we of course do not see a sphere; we don’t “see” a 3-dimensional view. What we “see” is a 2-dimensional cross section of the sky, as if we were looking at a movie screen. So our view is distorted, from 3 dimensions into 2. How does that fact change how we should interpret what we see?

Let’s explore what we actually “see”, to learn a few skills to interpret the data that we can collect.

We can start off by looking at the very simplest coordinate systems, to hone our skills at imaging the rotation from 3 dimensions to 1 or 2 dimensions.

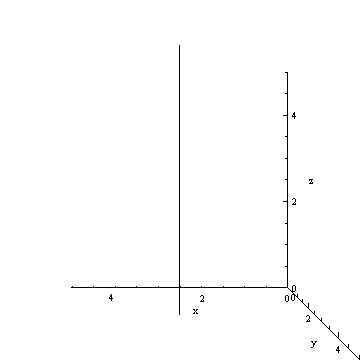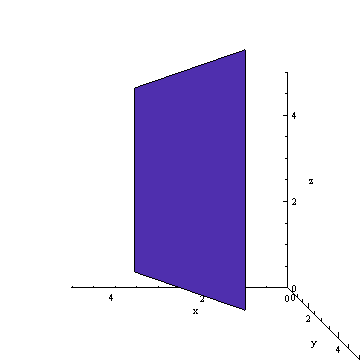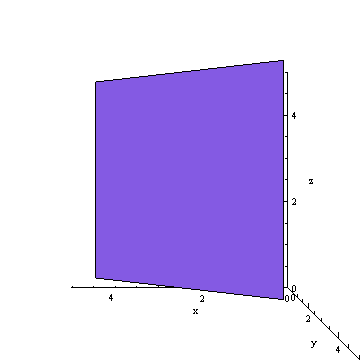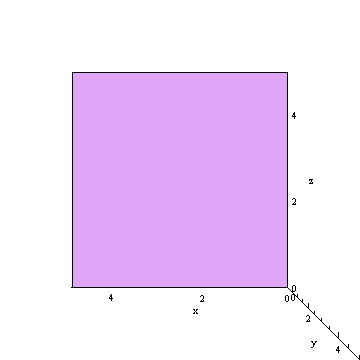
 A Line in 3D Space

As you can see, this is a line rotating through 90 degrees. The result is that we are looking at a one dimensional object from the point of view of the one dimension itself. So we have effectively reduced the dimension to 0, which is why we see a point. The same thing works for other objects in other dimensions.

A Circle in 3D Space

For example, here is a circle that is a two dimensional object. In a very similar fashion, we rotate through 90 degrees and the result is a line. This would work for any two dimensional figure, including squares, triangles, etc.

A 3D Sphere Reduced to 2D

Finally, we can see in this last graphic that a three dimensional object can be reduced to two dimensions. Now, here we first see that the different colors in the initial image represent the curved surface of the sphere. As the image changes, notice that the colors will eventually become just one shade of purple. This suggests that the object no longer has significant depth and is essentially a “flat” circle in two dimensions. (In reality, the object is very thin so as to even exist in our image.)

It’s important to note that in the first two animations we were simply altering our perspective. For the line, we looked at it from its end and it appeared to become a point. For the circle, we looked at if from its edge and it appeared to become a line. In a sense, this is what happens to a three dimensional object when observed from a great distance. The fine details which indicate the depth of the object are lost. So while in our animation we actually squeezed the sphere into a thin disk, the same effect would hold if we took a real ball and moved it very far away from you. It would start to look just like a circle.

2D to 3D

Another way of thinking about this is to try and go the other way. Imagine that we have a line which we suspect may be a two dimensional figure turned to look like a line. If we rotate it, we might expect a circle and we’d be wrong. Instead we have a square. But at the reduced level, it’s impossible to tell them apart. They both look like lines.

These examples serve to demonstrate some of the difficulties of understanding the “true” orbit of a celestial object, given that we usually only have observations measured  against essentially a 2D background of stars.

The astronomer Gauss, in thinking about how to find the asteroid Ceres, started with an understanding of how any object would appear against the background of stars, and from that data to determine its location in 3-dimensional space.